



"Les erreurs sont les preuves que l'on essaye !"


"Je ne perds pas, soit je gagne, soit j'apprends !"

Définition
Une fonction peut être vue comme une relation qui, à un élément de l'ensemble de départ, associe un seul élément de l'ensemble d'arrivée.
Exemples
La fonction illustrée ci-dessous agit comme une relation associant, à un nombre réel x un résultat équivalent à ce nombre augmenté de 3.
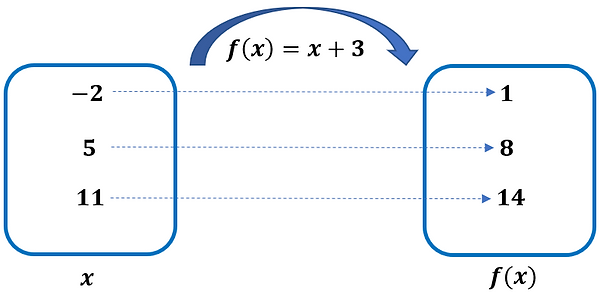
En revanche, la fonction représentée par le schéma ci-dessous associe, à un nombre réel x, un résultat équivalent au double de ce nombre diminué de 1.

Définition
Une fonction du type , avec a et b des nombres réels quelconques, est appelée une fonction du premier degré. La représentation graphique d'une telle fonction est une droite.
Définition
Soit une fonction f.
Soient un élément de l'ensemble de départ et un élément de l'ensemble d'arrivée de cette fonction, tel que
L'élément est appelé image de par la fonction f.
L'élément est appelé préimage de par la fonction f.
Exemples
Prenons une fonction définie par
Nous pouvons observer que 10 est l'image de 2 par cette fonction, puisque
En effet,
Prenons une autre fonction définie par
Nous pouvons observer que -1 est la préimage de 5 par cette fonction, puisque
En effet,
Les fonctions mathématiques du premier degré sont utilisées dans de nombreux domaines. Nous pouvons citer les situations de proportionnalité ou des problèmes d'économie comme l'évolution d'un capital placé à intérêts simples. L'évolution des coûts de production d'un objet, dépendant des coûts variables (v francs) et des coûts fixes (f francs) s'expriment également par une fonction du premier degré de la forme :
Pour acquérir et travailler les notions de base sur les fonctions du premier degré, je vous invite à consulter les documents théoriques et les vidéos associées, présentes dans cette section.